Signal to Noise Ratio (SNR) improvement for the fixed-point implementation of Biquads IIR filters.
Context
Digital filters are often designed to remove frequency content from an input stream. For example: removing upper bands signal energy before decimation to avoid spectral folding effects, or removing noise for the purpose a signal detection or audio enhancement.
Recursive IIR types of filters are preferred to FIR because the same attenuation is realized with approximately five-time less operations per samples. This choice results in power saving, more MHz free for other operations and less memory used in the filter state.
Adding cost and power constraints, the programs implementing IIR filtering are using fixed-point arithmetic’s. Compared to 32bits floating-point, the 16bits fixed-point format is saving power and memory. SIMD instructions found in CortexM4/M7 result in CPU-load efficiency.
Problem
IIR filters suffer from a sensitivity to truncations made in the recursive loop implementing the denominator of the transfer function. The purpose of this document is to explain how to limit the consequences of truncation on the resulting signal to noise ratio of the filtered stream.
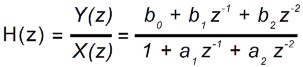
In the picture below we can see each multiplication between of data having A-bits and coefficients having B-bits result in A+B useful bit. The block “Q” is the quantizer. It truncates the results to the original register size of A-bits.
The truncation can be modelled as a noise generator inserted in the place of the quantizer. This noise is amplified when flowing in the recursive part of the filter. The coefficients a1,a2 give the amplification of this noise.
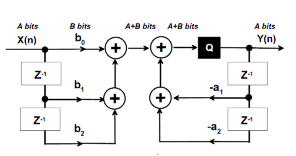
For practical explanations we will consider one Biquad designed as a low-pass filter for audio.
The resulting coefficients on numerator and denominator are :
The filter coefficients are quantized on 16bits:
When a 16-bits full-scale sine wave at 100Hz is processed through this filter, the resulting wave has a DC offset. The 10 most significant bits of the output are preserved from the corruption by the noise, and lowest 6 bits are lost due to the truncation noise.
Tools
We compute SNR in audio bands with this tool : http://firmware-developments.com/WEB/P6x/THDN/DOC/THDN.pdf
The program can take several type of input format and sampling rates. It delivers SNR in dB, dB(A) and dB(CCIR). It can cope with signal distortions related to jitter. You can tell it to compute SNR from a distorted data. It was qualified on real hardware.
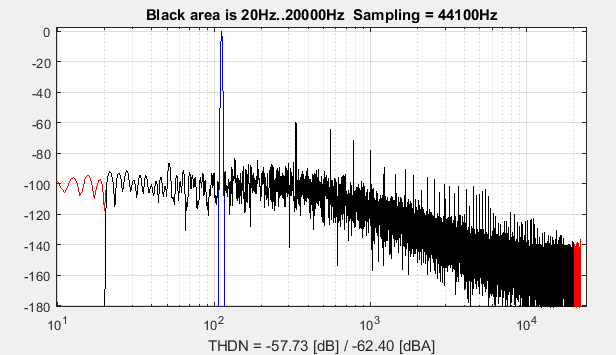
In our example the SNR result is 57dB, 62dB(A) computed from 20Hz to 20kHz :
Solution
The proposed signal processing enhancement is called Error Spectral Shaping (ESS) and is described in Ref [1] , [2]. It consists in computing, for each sample, the truncation error and resend this error to the next sample.
With this correction the transfer function of the noise has a zero placed at 0Hz and the noise spectrum close to Nyquist frequency (Fs/2) is amplified by 6dB.
In our example the SNR result is 87dB, 89dB(A) computed from 20Hz to 20kHz :
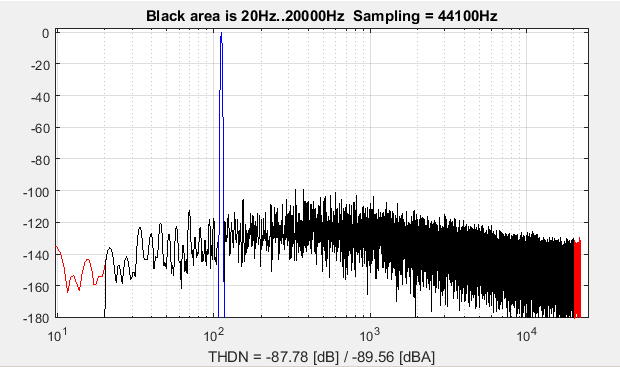
The complexity of the ESS truncation noise compensation adds minimal complexity (one addition) on top of the IIR filter operations, while improving the filtered output by about 6bits in our example.
For orders of magnitudes, our IIR implementation of Biquads using a CMSIS-compatible API is 31 cycles/sample on Cortex-M0 and 7.5cycles on Cortex-M4 (see http://firmware-developments.com/WEB/P6x/BIQ_M0/DOC/BIQ_M0.pdf).
References
1. The implementation of Recursive Digital Filters for High-Fidelity Audio, Journal of the Audio Engineering Society, Jon Dattorro, Vol 36, No 11, 1988 https://ccrma.stanford.edu/~dattorro/HiFi.pdf
2. AES standard method for digital audio engineering — Measurement of digital audio equipment, Revision of AES17-1991. https://www.ak.tu-berlin.de/fileadmin/a0135/Unterrichtsmaterial/KT-Labor_WS0809/1_ADDA/aes17.pdf
3. Roundoff Error Analysis of Digital Filters, Udo Zölzer, Journal of the Audio Engineering Society, Vol 42, No 4, 1994, http://firmware-developments.com/WEB/DOC/REF/IIR_noise_1.pdf
4. Importance of Precision on Performance for Digital Audio Filters, David Zaucha, AES Convention paper 5613, 2002, http://firmware-developments.com/WEB/DOC/REF/ZauchaIIR_AES.pdf
5. Finite Word length in Digital Filters: A review. H.J.Butterweck et al., EUT Report 88-E-205, Eindhoven University, 1988, http://firmware-developments.com/WEB/DOC/REF/FiniteWordlengthFilterEindhoven.pdf